Nguyên hàm từng phần là gì? Tổng hợp công thức tính từ cơ bản đến nâng cao đầy đủ nhất

Nguyên hàm là gì? Nguyên hàm từng phần là gì?

Trong toán học, cụ thể là môn giải tích (Hay còn được gọi là đại số), một nguyên hàm của một hàm số thực cho trước f là một hàm F có đạo hàm bằng f, nghĩa là, F′ = f. Quá trình tìm nguyên hàm được gọi là tích phân bất định.

Việc tìm một biểu thức cho nguyên hàm sẽ khó hơn so với việc tìm đạo hàm, và đôi lúc sẽ không thực hiện được. Tuy nhiên, bất kỳ hàm số liên tục trên đoạn hay khoảng từ giá trị a đến b, thì đều tồn tại nguyên hàm của hàm số đó trên đoạn/khoảng từ a đến b nêu trên.

Nguyên hàm từng phần là gì?

Phương pháp nguyên hàm từng phần thường được dùng để tìm tích phân bất định của các hàm số phức tạp, tức kết hợp nhiều loại hàm số trong một phép tính, gồm: Hàm số vô tỉ, hàm số logarit, hàm số mũ hay hàm số lượng giác.

Công thức tính nguyên hàm từng phần cơ bản

Cho hai hàm số u = u(x) và v = v(x) có đạo hàm liên tục trên K

=> Ta có công thức nguyên hàm từng phần: ∫udv = uv−∫vdu.

Chú ý: Ta thường sử dụng phương pháp nguyên hàm từng phần nếu nguyên hàm có dạng I=∫f(x).g(x)dx, trong đó f(x) và g(x) là 2 trong 4 hàm số: Hàm số logarit, hàm số đa thức, hàm số lượng giác, hàm số mũ.

Các bước tính nguyên hàm từng phần của ∫f(x).g(x)dx

Bước 1: Đặt

Công thức nguyên hàm từng phần đầy đủ nhất

Trong đó G(x) là một nguyên hàm bất kỳ của hàm số g(x)

Bước 2: Khi đó theo công thức nguyên hàm từng phần ta có:

∫f(x).g(x)dx=f(x).G(x)−∫G(x).f′(x)dx.

Chú ý: Khi I=∫f(x).g(x)dx và f(x) và g(x) là 2 trong 4 hàm số: Hàm số logarit, hàm số đa thức, hàm số lượng giác, hàm số mũ ta đặt theo quy tắc đặt u.

• Nhất log (hàm log, ln) - Nhì đa (hàm đa thức)

• Tam lượng (hàm lượng giác) - Tứ mũ (hàm mũ)

Tức là hàm số nào đứng trước trong câu nói trên ta sẽ đặt u bằng hàm đó. Như sau:

• Nếu f(x) là hàm log, g(x) là một trong 3 hàm còn lại, ta sẽ đặt:

• Tương tự nếu f(x) là hàm mũ, g(x) là hàm đa thức, ta sẽ đặt:

Xem thêm:

• Khái niệm và công thức của số hữu tỉ, sự khác biệt giữa số hữu tỉ và số vô tỉ là gì?
• Cách tính bán kính hình tròn đơn giản và bài tập tự luyện hiệu quả
• Dạy bé làm toán lớp 5 phép chia có dư và không dư dễ dàng nhất

Các bài tập mẫu có ứng dụng công thức nguyên hàm từng phần

Để dễ dàng áp dụng các công thức nguyên hàm từng phần trên vào các bài tập thực tế, Monkey xin giới thiệu một số bài toán từ cơ bản đến nâng cao sau đây.

Các dạng bài toán nguyên hàm từng phần thường gặp

Đây là 4 dạng bài toán nguyên hàm từng phần mà bạn dễ dàng bắt gặp chúng trong các đề thi mẫu hay đề thi chính thức.

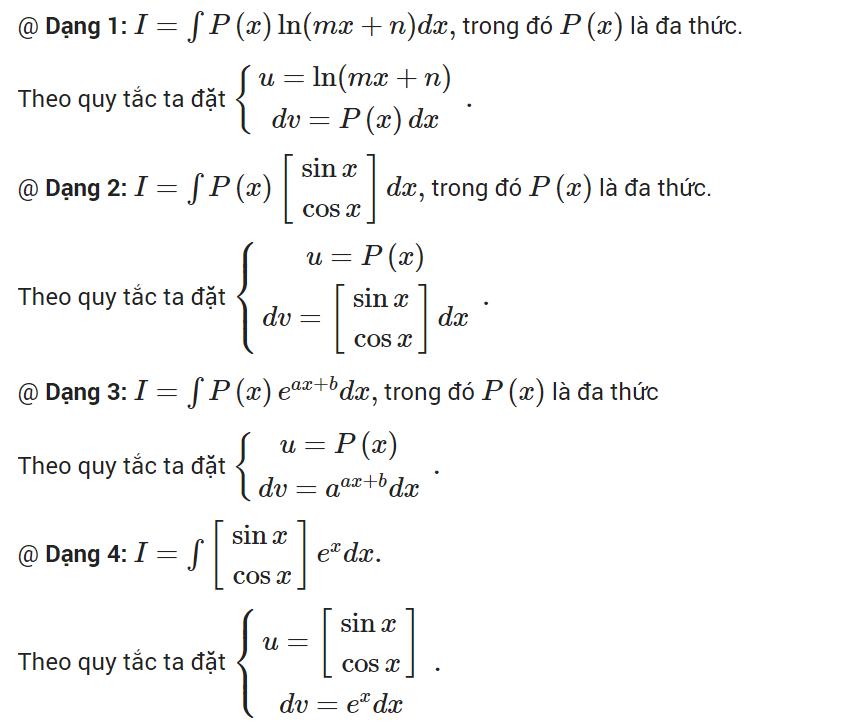
Một số bài toán mẫu có lời giải

Dưới đây là tổng hợp một số bài toán tính nguyên hàm từng phần có lời giải. Ba mẹ có thể tham khảo và cho các con luyện tập ngay tại nhà để củng cố kiến thức và rèn luyện kỹ năng làm bài toán nguyên hàm từng phần được tốt hơn.

Mách bạn mẹo nhỏ để tính nhanh nguyên hàm từng phần

Ngoài cách tính nguyên hàm từng phần cơ bản như trên, chúng ta cũng có thể áp dụng phương pháp đường chéo vào việc tính toán như sau.

Dạng 1: ∫f(x).e^(ax+b)dx

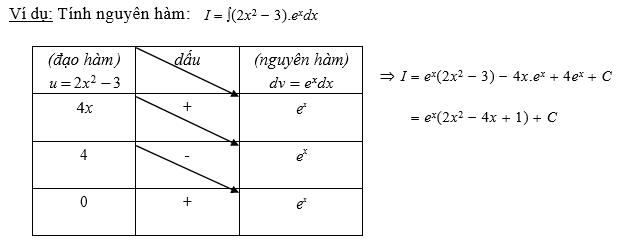
Dạng 2: ∫f(x).sin(ax+b)dx; ∫f(x).cos(ax+b)dx

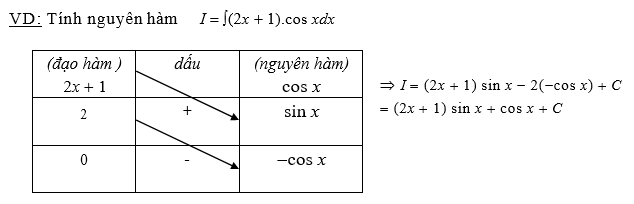
Dạng 3: ∫f(x).ln^n(ax b)dx

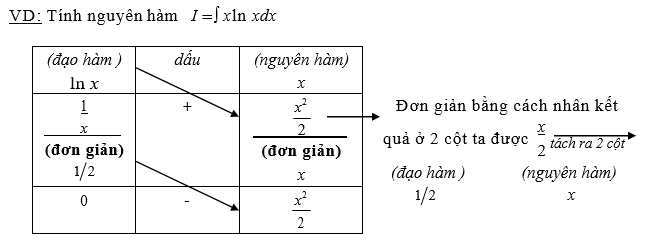
Dạng 4: Nguyên hàm lặp (Tích phân lặp)

Nếu khi ta tính nguyên hàm (tích phân) theo sơ đồ đường chéo mà lặp lại nguyên hàm ban đầu cần tính (theo hàng ngang) thì dừng lại luôn ở hàng đó, không tính tiếp nữa.

1. Dấu hiệu khi dừng lại: nhận thấy trên cùng 1 hàng ngang tích của 2 phần tử ở 2 cột (không kể dấu và hệ số) giống nguyên hàm ban đầu cần tính.

2. Ghi kết quả (nhân theo đường chéo) như các ví dụ trên.

3. Nối 2 phần tử (ở dòng dừng lại), có thêm dấu ∫ trước kết quả và coi gạch nối là 1 đường chéo, sử dụng quy tắc đan dấu.

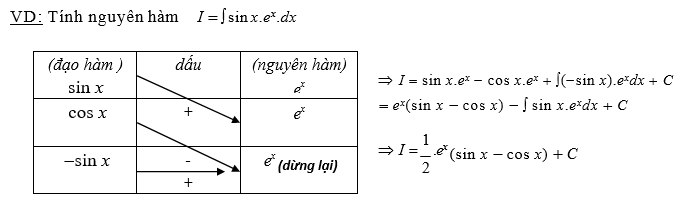
Tóm lại, để có thể ghi nhớ các kiến thức cũng như thành thạo cách giải bài toán nguyên hàm từng phần, bạn cần phải luyện tập nhiều hơn trong việc giải các dạng bài tập toán khác nhau. Chúc các bạn học giỏi môn Toán.

Ba mẹ muốn con học giỏi môn Toán, đồng thời cải thiện khả năng ngôn ngữ tốt hơn thì đừng bỏ qua ứng dụng Monkey Math nhé!

Xem thêm:

• Bí quyết giúp bé học giỏi toán lớp 4 hai đường thẳng song song
• Tổng hợp các dạng toán lớp 5 tỉ số phần trăm và hướng dẫn cách làm chi tiết
• Tổng hợp kiến thức và phương pháp học toán lớp 5 hiệu quả cho bé